

נשארים מעודכנים
הצטרפו לקהילת 'הגיע זמן חינוך' וקבלו עדכון שבועי עם כל מה שמורות ומורים צריכים לדעת
"הסתברות זה ממש קל", "הרעיון הזה ממש גאוני", "הבנתי מה זה חוקיות". אלו משפטי מתנה מתלמידים למורים למתמטיקה. לימוד נושא חדש במתמטיקה כולל התמודדות עם קשיים, בעיקר כשהלמידה נעשית מרחוק, אך כשמראים לתלמידים שהמתמטיקה סביבם בחיי היום-יום וממחישים להם את הדברים, הקושי הופך לאתגר ומסתיים בחוויה גם למורה וגם לתלמידים. אז איך עושים את זה?
אני מבקשת שנחזור לרגע לתקופה בה אנחנו היינו תלמידים, לשיעורי מלאכת יד או אומנות. לימדו אותנו למתוח קווים בעזרת סרגל, לקפל את הנייר לקבלת צורות חופפות, לשרטט ישר מקביל על ידי מדידה של מרחקים שווים מישר ועוד.
לא דיברו איתנו על מתמטיקה בשיעורים הללו ובטח לא על משפטים בגיאומטריה, אבל כשהגענו ללמוד על פונקציה קווית, למשל, היה לנו ברור למה מספיקות בטבלת הערכים 2 נקודות על הישר והבנו את המשמעות של "משוואת ישר על פי שתי נקודות על הישר".
ייתכן שכבר אז נכנס לתת-המודע שלי הרעיון שאפשר "להרגיש את המתמטיקה". לאורך השנים, הוראת המתמטיקה אפשרה לי לחזור לרגעים בחיי היום-יום בהם "מרגישים" מתמטיקה או לחפש מודלים שיאפשרו לי להמחיש לתלמידים נושאים מתמטיים שונים. ההתנסות עם יישום המתמטיקה, מביאה את התלמידים להבנה טובה יותר של הדברים - להבנה של המשמעות, ומאפשרת להם לחקור מקרים פרטיים כדי להגיע להכללה. הדבר אינו מחליף כמובן הוכחה רשמית של ההכללות, אבל התלמידים בהחלט מקבלים מוטיבציה להוכיח.
חיזוקים לעמדתי קיבלתי ממחקרים שונים אשר עמדו על היתרונות של המחשה בנוגע להוראת המתמטיקה. כך למשל, מחקר משנת 2011 (שליטא, פרידמן, הרתאן) הראה עליה במוטיבציה והתעניינות אישית של תלמידים כתוצאה משימוש באמצעים חזותיים בהוראת המתמטיקה. גם בדוח של משרד החינוך משנת 2010 התייחסו לעניין. ההמחשה יכולה להיות באמצעות תמונה, באמצעות יישומון מחשב, שימוש בחיי היום-יום ועוד.
במבט לאחור, שיעורים בהם התלמידים "נוגעים במתמטיקה" ומרגישים אותה, הם שיעורים חווייתיים גם עבורי כמורה וגם עבור התלמידים. עבור תלמידים ברמות הגבוהות ניתן להשתמש במודלים כשיעורי חקר – גילוי של תופעה מתמטית ועבור תלמידים מתקשים, ניתן להוסיף לפעילות שאלות מכוונות.
אציג מספר דוגמאות שאספתי במהלך השנים, בעזרתן התלמידים יכולים "להרגיש מתמטיקה". חלק מהרעיונות קיבלתי ממדריכות שעוררו בי השראה, כמו ד"ר רותי רייז, ניצה שיאון, איריס זודיק ועוד.
כולנו מקבלים במדיה "חידות מתמטיות", בסגנון הבא ונהנים לפתור אותן:
ייתכן והיינו נהנים פחות לו ההוראה הייתה "פתרו את המשוואות הבאות: 2x=24, x+y=15 וכן הלאה. בשלב זה של השנה, התלמידים שלי כבר לא חוששים מהמילה "משוואה" ומצליחים לפתור משוואות בדרך אינטואיטיבית.
כאשר תלמידיי נדרשו לפתור משוואה על ידי ביצוע אותה פעולה על שני אגפי המשוואה, שיחקנו (בדמיון) בנדנדה בגן המשחקים. דמיינו שהיא מאוזנת כאשר מושיבים מבוגר בצד אחד ושני ילדים בצד השני ואז השתעשענו בניסיונות שונים להושיב עוד מבוגרים וילדים על הנדנדה ולשמור על איזון.
גם את הנושא "חוקיות" ניתן להרגיש, במיוחד בתקופה מאתגרת בה מדברים על "מקדם הדבקה". הלמידה מרחוק זימנה אפשרות ללמד את אותם הדברים, אבל אחרת. במקום לשרטט על הלוח, ניתן להיעזר במצגות שימחישו את המשמעות של "מקדם הדבקה 1" והחוקיות המסתתרת מאחוריו. כמו באיור כאן.


באחד השיעורים ביקשתי מהתלמידים להביא לשיעור מספריים. כל תלמיד קיבל דף והיה עליו לקפל אותו לשניים, כך שאחת הצלעות מהמסגרת "תתקפל על עצמה". לאחר מכן, היה עליהם לשרטט קטע המחבר בין נקודה על קו הקפל לנקודה על המסגרת ולגזור. דנו בסוג המשולש שהתקבל ומדוע הוא חייב להיות ישר זווית.
כעת נתבקשו התלמידים לפתוח את המשולש כך שלא יהיו קיפולים. דנו שוב במשולש שהתקבל (שווה שוקיים). הפעם המשימה הייתה לחקור מה מיוחד במשולש שווה שוקיים ולבדוק האם זה מתקיים גם במשולשים של החברים בקבוצה / כיתה או רק במשולש שאני גזרתי. התלמידים נדרשו לשכנע את חבריהם באמצעות נימוקים מתמטיים המתבססים על ידע קודם שצברו (למשל, חפיפת משולשים).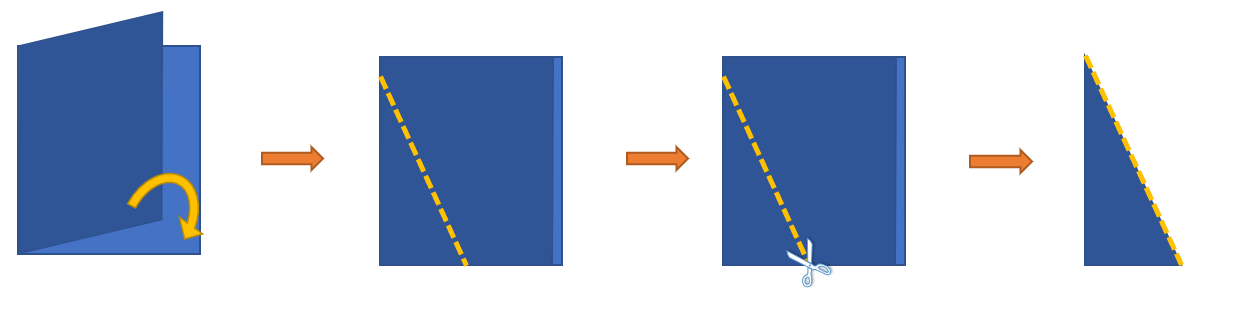
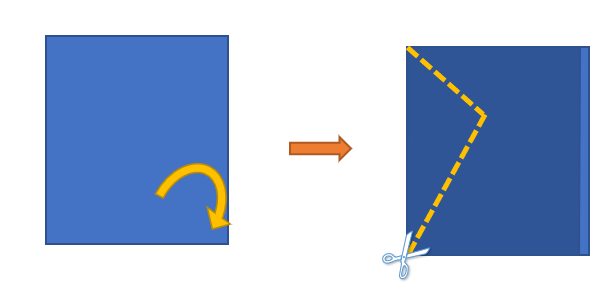
פעילות דומה ניתן לבצע עם דלתון (אם משרטטים משולש על קו הקפל במקום קטע) או עם מעוין, במידה ומקפלים את הדף ל-4 וגוזרים את "הפינה הסגורה".
ומה לגבי הסתברות? ניתן להסביר לתלמידים שמדובר ביחס בין מספר האפשרויות הרצויות למספר האפשרויות הקיימות או שאפשר להגיע לכיתה עם קופסה אטומה המעוררת סקרנות של התלמידים ולשאול את התלמידים מספר שאלות, כמו: מה הסיכוי שאוציא דג מהקופסה? מה הסיכוי שאוציא עיפרון מהקופסה? מה הסיכוי שאוציא סוכריה מהקופסה?
הניסיון שלי הראה, שלאחר שהתלמידים צוחקים מהשאלה על הדג, הם משתמשים במילים "זה תלוי". מכאן הצלחת השיעור תלויה בניהול הדיון – במה זה תלוי? ואז עולים העניינים המהותיים בהבנת מושג ההסתברות: האם יש בכלל עפרונות בקופסה? (אם אין – סיכוי 0, אם יש רק עפרונות - סיכוי של 100%). כמובן שהתעלומה לגבי תוכן הקופסה נפתרת רק בסוף השיעור, אך השאלות ממשיכות להישאל.
המורה: "נניח שיש בקופסה סוכריות. מה הסיכוי להוציא סוכריה בטעם תות?" התלמידים שואלים שאלות אינטואיטיביות, כגון: "יש סוכריות בטעם תות? כמה סוכריות בטעם תות יש? כמה סוכריות יש בסך הכל?" כל שנותר לי לעשות כמורה הוא לסכם את השאלות האינטואיטיביות להגדרה מהי הסתברות.
התלמידים שותפים פעילים בשיעור והסקרנות לגלות מה בקופסה מעוררת את הקשב שלהם. התפקיד שלי הוא רק לנהל את הדיון. הסמכות לאשר את הידע נמצאת בידי התלמידים.
אחד הנושאים שאני הכי אוהבת לתת לתלמידים "להרגיש" הוא סימון נקודות במערכת צירים. כל מה שדרוש הוא רצפה משובצת, כזו שנמצאת כמעט בכל כיתה ונקודה המוסכמת כנקודת מוצא. המשימה של התלמידים היא לכוון אותי מנקודת המוצא לעבר מטרה מסוימת בכיתה (למשל, תיק של תלמיד המונח על הריצפה). כמובן שעד שהתלמידים לא מדייקים במושגים המתמטיים אני לא מגיעה ליעד. כך למשל, השימוש במילה "צעדים" לא מתאים, כיוון שניתן ללכת בצעדים קטנים לעומת גדולים, אך "משבצת" יכולה לשמש כיחידת מידה.
בהמשך אנו מדברים על תכנת הניווט "וויז", קווי אורך ורוחב במפה, על מסך מגע ועל מדפסת – כולם עושים שימוש כזה או אחר במערכת צירים.
בימים אלו, בהם המחשב והמדיה נמצאים בבסיס הלמידה, ניתן גם להיעזר ביישומונים שונים להמחשה וכן בסרטונים מהרשת. כמובן שאפשר גם להכין לבד. כאשר התלמידים "מרגישים מתמטיקה" הם מעורבים יותר בשיעור ולנו המורים, נותר רק ללוות אותם בדרך לגילוי האמת המתמטית.

