בקליניקה של הרופא או על שטיח מעופף: המתמטיקה של החיים האמיתיים

אין זה סוד, רבים מהתלמידים לא אוהבים מתמטיקה. יתרה מכך, הם חשים תחושת ניתוק לנוכח המספרים המאיימים. מתברר שאחת הסיבות לכך היא התרגילים שנותנים להם לפתור. 

המתמטיקה הייתה שם כבר לפני עשרות אלפי שנים, והחלה בכלל מצורך פרקטי, כשבני האדם עסקו בחישוב ובמדידה של כמויות, מבנים ומרחבים. אך עם שינויים שחלו בנורמות חברתיות ובגישות פילוסופיות, עלתה קרנה של המתמטיקה המופשטת, זו הרחוקה משימושי היום יום. אותה מתמטיקה היא זו הנלמדת בבתי הספר, ומשום שהיא עוסקת בייצוגים מופשטים, נוצרה בקרב תלמידים ומבוגרים רבים התפיסה השגויה שהמקצוע לא שימושי. כתוצאה מכך תלמידים ניגשים למתמטיקה בחוסר עניין ומתקשים בהבנת החומר. וכך, מורים רבים למתמטיקה מרגישים שהם צריכים לעשות 'שמיניות באוויר' כדי לגרום לתלמידים להתחבר למקצוע.

פרופסור פולין ווס חקרה את מאפייני הוראת המתמטיקה בהולנד וגילתה שסוד ההצלחה טמון בהקשר: משימות בעלות הקשר לחיים האמיתיים, הכוללות פחות סימנים ושפה מתמטית ויותר מלל וייצוגים ויזואליים, גורמות לתלמידים לתפוס מתמטיקה כיותר מועילה ושימושית במגוון מצבים חדשים. ההרגשה הזו נוטה להגביר את המוטיבציה ללמידה.

הולנד, אהובתי

במרבית המדינות נעשה שימוש מוגזם בתרגילים מופשטים, ושימוש מועט מידי בתרגילים שיש להם הקשר הלקוח מן המציאות. לא כך הדבר בהולנד. מחקרים בינלאומיים מראים שבמערכת החינוך בארץ הכפכף משתמשים הרבה יותר במשימות שיש להן מהיומיום. משימות כאלה אינן רק מילוליות, אלא גם מוצגות באופן חזותי על ידי איורים, תמונות, דיאגרמות ועוד. לא מדובר בתופעה חדשה, כבר במאה ה-16 בהולנד השתמשו פוליטיקאים, בעלי ממון וסוחרים ביישומים מתמטיים פשוטים כמו המרת מידות ומטבעות כדי לנהל את העסקים שלהם ואת החברה. בהתאם לכך, מסלולי המתמטיקה בחלק מהאוניברסיטאות לימדו יישומים מתמטיים בתחומים שונים כמו ימאות ואדריכלות מבצרים (כן כן, מבצרים).

לעוד כתבות על לימוד מתמטיקה עם טוויסט:

• האם שנת הקורונה היא תחילתו של מהפך?
• איך תגרמו לתלמידים לרצות ללמוד מתמטיקה?
• איך מצליחים במתמטיקה? הכל עניין של תפיסה
• איך ללמד מתמטיקה ומדעים בלי להפחיד את התלמידים?
• למדו את תלמידיכם שפה ולא תרגיל

אז איך אפשר לעודד תלמידים לתפוס את המתמטיקה כמשמעותית באמצעות התרגילים שהמורה מביא לשיעור? דמיינו שאתם צריכים ללמד את התלמידים שלכם חילוק של מספר מעורב בשבר ובוחרים בתרגיל הבא: ¼ :  ½ 3

הרי לכם חמישה אופנים, יצירתיים יותר ופחות, שבהם אפשר להציג תרגילים מתמטיים:

• משימות טהורות או חשופות: התרגיל שלמעלה, כמו רבים אחרים, כתוב בשפה מתמטית. הוא לא מייצג שום דבר מלבד את המספרים עצמם. התרגול של משימות כאלה נועד לגרום לתלמידים לתרגל באופן מכאני ולשנן חוקים מתמטיים. התלמידים אמנם מבינים שהם צריכים לתרגל משימות כאלה כדי לעבור מבחנים אבל הם בדרך כלל לא תופסים אותן כשימושיות או רלוונטיות.

• משימות בעלות הקשר מתמטי: אפשר להציג את התרגיל באמצעות סרגל באורך שלוש יחידות וחצי וסרגל באורך רבע יחידה לצד השאלה "כמה יחידות קטנות אפשר להכיל בתוך היחידה הגדולה?". בשונה ממשימות טהורות, משימות עם הקשר מתמטי הן לרוב חזותיות ומתייחסות לגופים מתמטיים ולמאפיינים שלהם. בנוסף, הן בדרך כלל לא עושות שימוש בשפה מתמטית.

• משימות מחופשות: "כמה רבעי שעה יש בשלוש שעות וחצי?" - בניסוח הזה, אותו תרגיל מלמעלה מוצג בהקשר שמעניק ליחידות ולממדים שלו משמעות. למרות זאת, בעודו מגרד בראשו התלמיד עשוי לשאול את עצמו: מה הטעם במשימה הזאת? לא ברור למי או למה התרגיל יכול לעזור, ואיזה אירוע מייצגות אותן שלוש השעות וחצי. לתרגיל הזה יש הקשר לא מוגדר. במשימות כאלה לא מתוארים שחקנים אמינים - אנשים או מוסדות עם בעיה שדורשת פתרון. למרות שהן לא נתפסות כשימושיות, למשימות מחופשות עדיין יש יתרונות מבחינת הדרישה הקוגניטיבית מהתלמיד. הן גורמות לו לקרוא מילים במקום סימנים, מנגישות את התרגיל ומגבירות את העניין של התלמיד.

• משימות בעלות הקשר ריאליסטי: כדי לשפר משימה מחופשת, צריך לקשר אותה למציאות. ניקח את המשימה שהוצגה קודם, "כמה רבעי שעה יש בשלוש שעות וחצי?", ונקשר אותה למציאות: "לרופא במרכז רפואי נקבעו פגישות ייעוץ מהשעה 8:30 ועד 12:00. הרופא מקדיש לכל מטופל רבע שעה. כמה מטופלים יכול הרופא לפגוש בפרק זמן זה?". משום שרוב התלמידים ביקרו אצל רופא בחייהם, הם יחוו את התרגיל כאמיתי ולפיכך שימושי. אפשר גם להטמיע את אותו תרגיל בהקשר ריאליסטי שהתלמידים לא התנסו בו, כמו חקר לווייתנים, או מסעו של אלאדין על שטיח מעופף. התלמידים יהיו מסוגלים לדמיין אותם ולתפוס אותם כמציאותיים. בדרך כלל, משימות בעלות הקשר ריאליסטי מתארות פעילויות בשעות הפנאי או עבודה של בעלי מקצוע, מה שמדגים כיצד מתמטיקה שימושית בתחומים מגוונים.

• משימות בעלות הקשר אותנטי: משימות כאלה נטועות בהקשר אמיתי וכוללות "הוכחות" או נתונים ששימשו לתיעוד התופעה או המקרה המתוארים. צילומים, נתוני תקציב של משרד ממשלתי או מידות של ממצאים ארכאולוגיים – הן דוגמאות למשימות כאלה. משימות בעלות הקשר אותנטי נוטות להיות מורכבות יותר ממשימות ריאליסטיות, כיוון שהמציאות נוטה להכיל מורכבות. כך למשל, מטופלים מסוימים עשויים להזדקק לתור של בן חצי שעה. כמו כן, הרופא עשוי לצאת להפסקת התרעננות באמצע יום העבודה. אם כך, אפשר להפוך את המשימה מקליניקת הרופא לבעלת הקשר אותנטי על ידי שימוש בנתונים אמיתיים מקליניקה של רופא והכנסת אילוצים נוספים למטלת קביעת התורים. המורה יכול לספק לתלמידים צילום של דף אמיתי מיומנו של הרופא בו רואים שהיומן תפוס עד השעה 8:30 ומהשעה 12:00 ואילך.
  
  דוגמה למשימה מסוג זה: "לפניך דף מיומן התורים של ד"ר יוספוביץ'. בדף היומן ניתן לראות את השעות בהן הד"ר נמצא בכנס מקצועי ואת השעות בהן יש לתאם עבורו תורים. הרופא מקדיש לכל מטופל רבע שעה. לאחר כל בדיקה, משכתב הרופא את סיכום הבדיקה במשך 6 דקות. כמה מטופלים יוכל הרופא לבדוק ביום ד' הבא?"

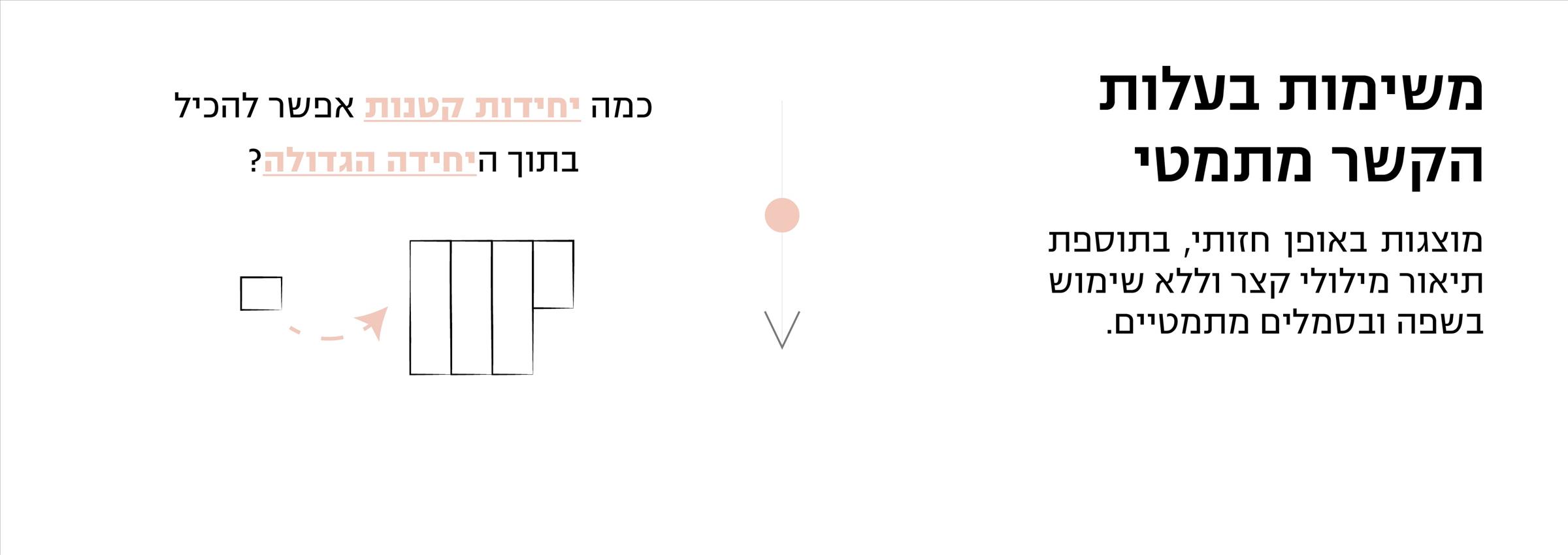
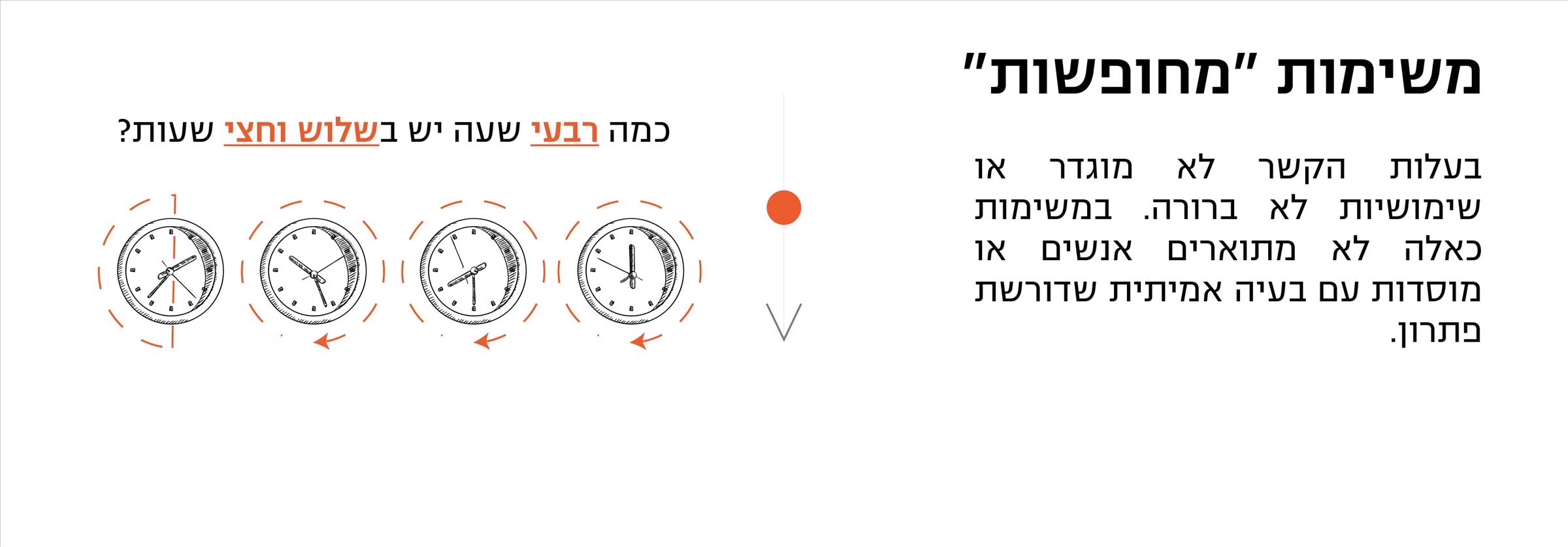
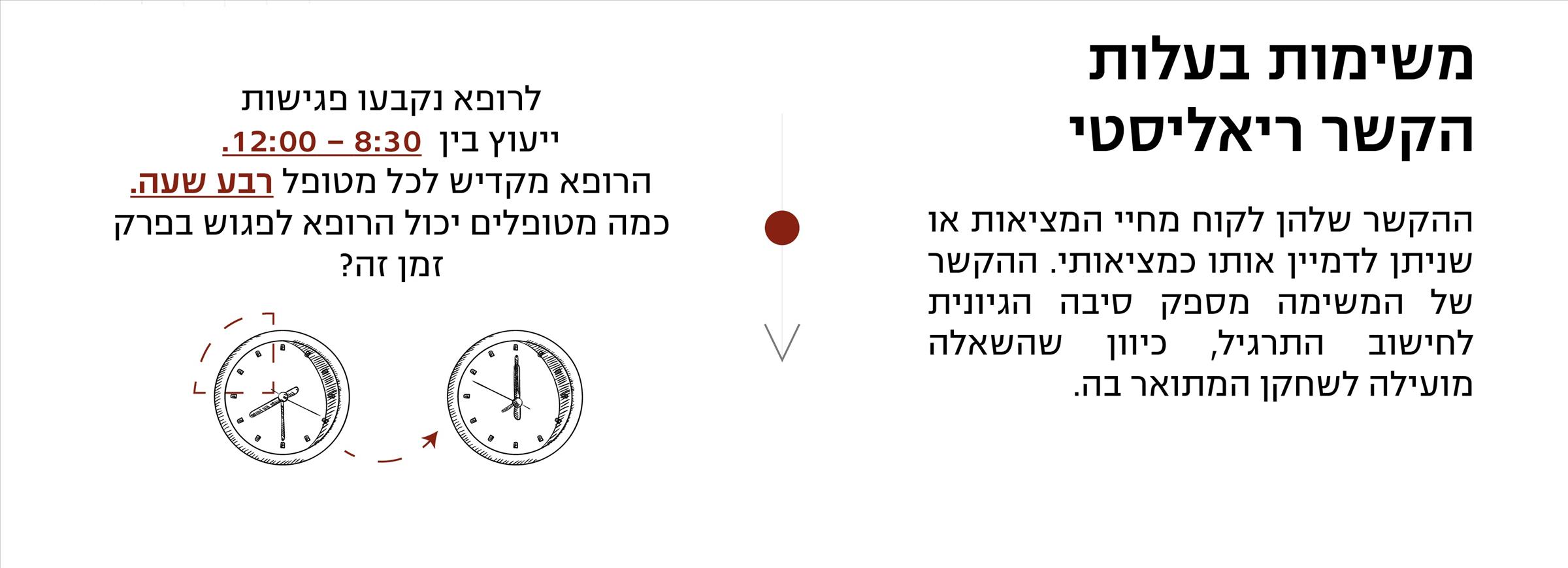
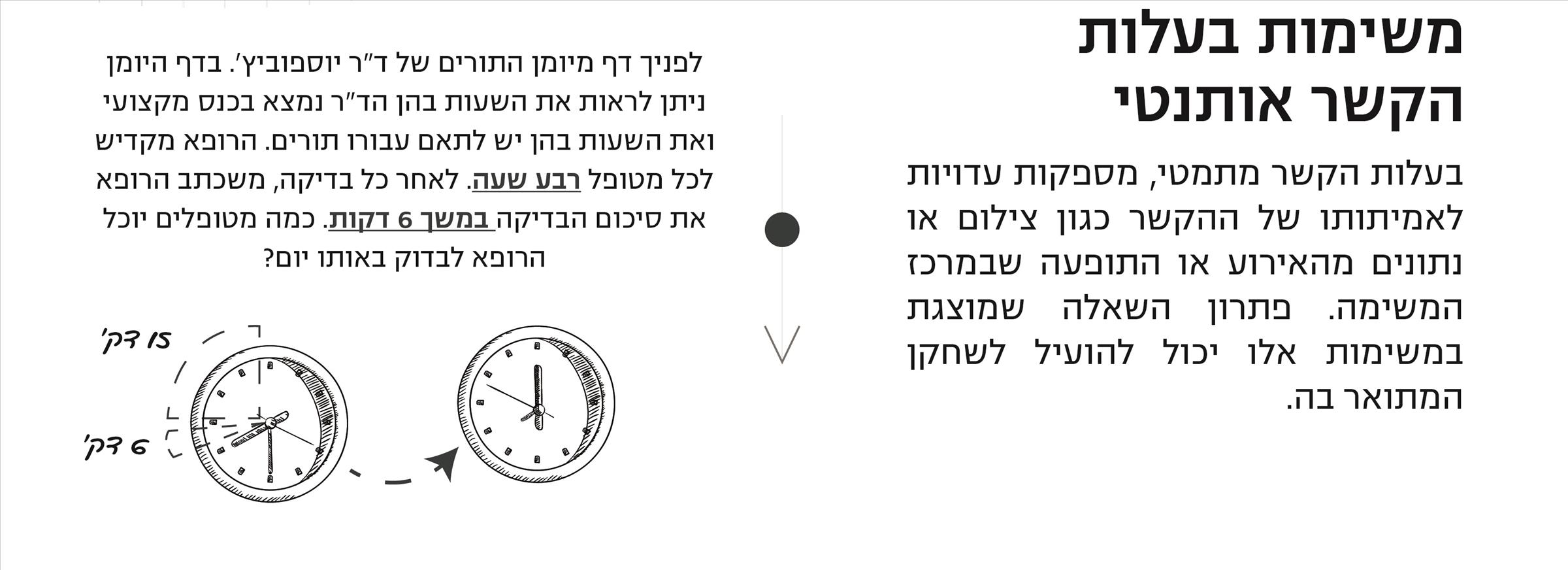
שימו לב: גם בקטגוריה האחרונה חשוב לבדוק אם השאלה שמוצגת במשימה יכולה להועיל לתמונת המצב או שהיא יעילה רק עבור התרגול המתמטי. אם התשובה השנייה היא הנכונה – אופס, למשימה יש הקשר אותנטי אבל השאלה שבה לא שימושית. המשימה האחרונה אכן מספקת מספק סיבה הגיונית לחישוב התרגיל - הרופא צריך לדעת כמה מטופלים הוא יוכל להספיק לראות, בהתחשב באילוציו ושגרת העבודה שלו.

אם כן, כמורים, חשוב שנשאל את עצמנו באיזה הקשר, אם בכלל, כדאי להציג את התרגיל שאנחנו מתכננים ללמד – האם ההקשר נותן ערך מוסף לביצוע התרגיל, או נכפה עליו באופן מאולץ רק לשם פתירתו? במקרה השני עדיף להימנע מהקשר יצירתי האוחז במציאות; שנית, במקום להמציא נתונים של בעיה, מומלץ למצוא נתונים אמיתיים של בעיה מעניינת מחיי היומיום, ולהציג אותה לתלמידים לפני שמלמדים פרק חדש. התלמידים ינסו לפתור אותה, ויבינו שלשם כך עליהם ללמוד משהו חדש, והפלא-ופלא: הרי לכם מתמטיקה שימושית.

הכנו לכם גרסה להדפסה של חמש הדרכים להצגת תרגיל מתמטי. מוזמנים להוריד אותה ממש כאן. 

יש לכם שיטה יצירתית משלכם ללימוד מתמטיקה? ספרו לנו עליה!